k-Disjunctive Normal Form functions

The k-Disjunctive Normal Form (k-DNF) functions are synthetic boolean functions that present different challenges for evolutionary learning in terms of number of attributes, size of the training set, overlapping and noise, among others.

In a space of d variables, the k-DNF functions have a following structure:

${\displaystyle T_1\vee T_2\vee ...\vee T_r}$

where r is the number of disjunctive terms and each term T_x represents the conjunction of k out of d variables (x₁, x₂, ..., x_d). In boolean k-DNF functions a value of 0 or 1 is associated to each variable x_i. The following is an example of k-DNF function in a space of 10 variables (d), with 3 terms/rules (r) using 4 variables/attributes (k) each.

${\displaystyle (x_1\wedge x_5\wedge \neg x_7\wedge x_8)\vee (x_1\wedge \neg x_3\wedge \neg x_6\wedge x_7)\vee (x_1\wedge x_2\wedge \neg x_6\wedge x_8)}$

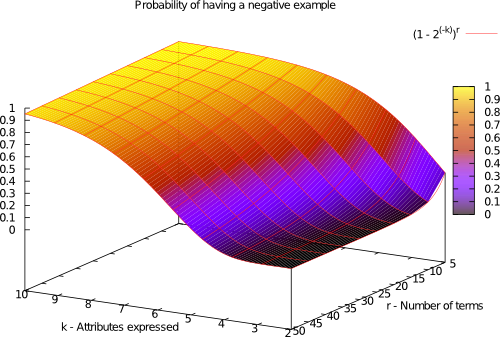
The difficulty of learning a k-DNF function depends on the class imbalance and rule overlapping. The probability of having a negative example follows the following distribution:

k-DNF Generator

You can download the C++ source code of a k-DNF problem generator. The generator's input are the d, k, r parameters, the amount of noise and a random seed (to be able to reproduce the same sets). Instead of a complete k-DNF problem, the generator can produce just a random sample, which is useful for problems with a large amount of attributes and instances.

Datasets

Two different k-DNF datasets have been used in our experiments:

Download simple set: group1.tar.gz [2.4 GiB]
The set includes 990 problems, 10 for each configuration with the parameters: d = [20], k = [2,3,4,5,6,7,8,9,10], r = [1,5,10,15,20,25,30,35,40,45,50]. These datasets have been used in Franco2010a.

Download noisy set: group2.tar.gz [2.3 GiB]
The set includes 1800 problems, 5 for each configuration with the parameters: d = [10,20], k = [2,3,4,5,6,7,8,9,10], r = [1,5,10,20,40].
Each problem contains a certain ratio n of noise, where n = [0, 0.01%, 0.05%, 0.10%].

For any comments or questions about k-DNF problems or datasets in this website please send an e-mail to jaume.bacardit.

Publications

• DOI slides BibTeX
  M.A. Franco, N. Krasnogor, J. Bacardit
  Analysing bioHEL using challenging boolean functions
  in Proceedings of the 12th annual conference comp on Genetic and evolutionary computation - GECCO '10, p.1855, Portland, Oregon, USA, 2010

  @INPROCEEDINGS{Franco2010a,
    title = {Analysing bioHEL using challenging boolean functions},
    author = {Franco, Maria A. and Krasnogor, Natalio and Bacardit, Jaume},
    year = 2010,
    doi = {10.1145/1830761.1830817},
    booktitle = {Proceedings of the 12th annual conference comp on Genetic and evolutionary computation - GECCO '10},
    pages = {1855},
    address = {Portland, Oregon, USA}
  }